Полярный угол – это угол, который определяется в полярной системе координат. Полярная система координат представляет собой двумерную систему, в которой плоскость разбита на радиальные лучи, называемые радиусами, и окружности, называемые полярными линиями.
Полярный угол измеряется в градусах или радианах и задается относительно положительного направления радиуса. Это значит, что полярный угол отсчитывается от положительного направления оси Ox по часовой стрелке или против часовой стрелки.
Угол в полярной системе координат обычно обозначается символом θ (тета). Он определяется с помощью радиуса, который проводится от начала координат (точки O, центра полярной системы координат) до точки на плоскости. Угол задается расстоянием между радиусом и положительным направлением оси Ox.
Полярный угол имеет значения от 0 до 360 градусов или от 0 до 2π радиан. Поэтому при измерении полярного угла нужно учитывать, что он может принимать значения в диапазоне от 0 до 360 градусов или от 0 до 2π радиан.
Полярный угол: определение и смысл
Полярный угол – это меряющая величина, характеризующая отклонение направления луча относительно направления оси полярных координат в плоскости. В математике и физике, полярный угол является одним из способов задания точки на плоскости.
Определение полярного угла тесно связано с системой полярных координат, представляющей собой двумерную систему координат, в которой точка задается парой чисел – радиусом-вектором и полярным углом. Полярный угол измеряется относительно положительного направления оси абсцисс и может быть положительным или отрицательным.
Полярный угол имеет важное значение не только в математике, но и в физике, астрономии, географии и других науках. Он используется для описания направлений, вращений, поляризации света, а также в решении задач, связанных с геометрическими и физическими явлениями на плоскости.
Смысл полярного угла заключается в том, что он позволяет определить положение точки относительно начала координат и направления оси абсцисс. Он также определяет угол между направлением луча из начала координат к точке и положительным направлением оси абсцисс.
Важно отметить, что полярные углы могут быть преобразованы в декартовы координаты и наоборот при помощи формул преобразования координат. Это делает их удобным инструментом для работы с геометрическими проблемами на плоскости.
В общей геометрии
В общей геометрии полярный угол представляет собой угол между положительным направлением оси и лучом, проведенным из начала координат (полярного центра) в точку на плоскости. Полярный угол измеряется в радианах или градусах и может быть положительным или отрицательным, в зависимости от направления вращения луча против или по часовой стрелке.
Основные свойства полярного угла в общей геометрии:
Положительное направление полярного угла совпадает с направлением положительного вращения луча от оси.
Полярный угол может быть представлен в виде десятичной или дробной десятичной дроби, в виде процентов, градусов, минут и секунд.
Обратное значение полярного угла, то есть угол, который дополняет данный угол до 360 градусов, называется сопряженным углом.
Полярный угол может быть отрицательным, если он измеряется в направлении против часовой стрелки.
В общей геометрии полярный угол широко используется для описания положения точек в полярной системе координат, где точка определяется радиус-вектором (расстояние от начала координат до точки) и полярным углом.
В полярной координатной системе
Полярная координатная система — это система, которая позволяет задавать точки с помощью полярного угла и радиуса.
Полярный угол — это угол, образованный между положительным направлением оси абсцисс и лучом, соединяющим начало координат с точкой.
Особенностью полярной координатной системы является то, что она позволяет задавать точки в плоскости без использования прямоугольных координат x и y. Вместо этого точка задается парой чисел (r, θ), где r — радиус, а θ — полярный угол.
Полярный угол измеряется в радианах и может принимать значения от 0 до 2π. При этом 0 соответствует положительному направлению оси абсцисс, а положительные значения полярного угла считаются против часовой стрелки.
В таблице ниже приведены основные свойства полярной координатной системы:
| Радиус r | Полярный угол θ |
|---|---|
| Положительное число | 0 ≤ θ ≤ 2π |
| 0 | Не определен |
| Отрицательное число | π + θ |
Таким образом, полярный угол является важным понятием в полярной координатной системе и позволяет задавать точки в плоскости с помощью полярных координат.
Как измерить полярный угол?
Полярный угол измеряется в градусах (°) или радианах (rad) и используется для определения положения точки на плоскости относительно начала координат.
Существуют несколько способов измерения полярного угла:
- Использование градусов: для измерения полярного угла в градусах необходимо провести луч, исходящий из начала координат и заканчивающийся на точке. Затем необходимо определить угол между положительным направлением оси X и данной точкой. Угол измеряется против часовой стрелки (по положительной части окружности) и может принимать значения от 0° до 360°.
- Использование радианов: для измерения полярного угла в радианах также необходимо провести луч из начала координат до точки. Затем необходимо найти длину дуги окружности, отсчитанную от положительной оси X до данной точки, и разделить ее на радиус окружности. Полученное отношение и будет значением полярного угла в радианах. Угол также измеряется против часовой стрелки и может принимать значения от 0 до 2π (или от 0 до 360° соответственно).
Измерение полярного угла является важной частью анализа данных и решения различных задач в физике, математике и других науках.
Основные свойства полярного угла
1. Измерение в градусах и радианах
Полярный угол измеряется в градусах или радианах, и в каждой системе есть свои особенности.
В градусной системе, один полный оборот равен 360°, а каждый градус делится на 60 минут и каждая минута делится на 60 секунд. Например, 45° равны 45 градусам, 30 минутам и 0 секундам.
В радианной системе, один полный оборот равен 2π радиан или примерно 6,28318 радиан. Для преобразования из градусов в радианы можно воспользоваться формулой: радианы = (градусы * π) / 180.
2. Положительные и отрицательные углы
Полярные углы могут быть положительными или отрицательными, в зависимости от направления их вращения относительно начальной точки. Если угол вращается против часовой стрелки, он считается положительным, а если по часовой стрелке – отрицательным.
3. Отражение полярных углов относительно осей
Полярные углы могут быть отражены относительно оси x или оси y. Например, если мы имеем угол α, то его отражение ω по оси x будет равно 180° — α, а отражение ω по оси y будет равно -α.
4. Полярный угол и тригонометрические функции
Полярные углы тесно связаны с тригонометрическими функциями (такими как синус, косинус, тангенс и т. д.). Используя значения этих функций, можно определить координаты точки на плоскости, заданной полярным углом и радиусом.
5. Полярный угол и геометрические построения
Полярные углы широко используются в геометрических построениях, включая построение окружностей, эллипсов и других фигур. Используя полярные углы, можно контролировать форму и расположение этих фигур.
6. Ограничения полярного угла
Полярный угол ограничен в рамках одного оборота (360° или 2π радиан). Однако, в некоторых случаях, полярные углы могут быть превышены или использоваться для представления углов, больших чем один оборот.
| Система измерения | 1 полный оборот | Примеры |
|---|---|---|
| Градусы | 360° | 45°, 90°, 180° |
| Радианы | 2π радиан или примерно 6,28318 радиан | π/4 радиан, π/2 радиан, π радиан |
Значение полярного угла от 0 до 180 градусов
Полярный угол – это угол между положительным направлением оси x и лучом, исходящим из начала координат и заканчивающимся в точке с заданными радиусом и углом.
Значение полярного угла может варьироваться от 0 до 180 градусов. В этом диапазоне полярные углы можно классифицировать на следующие типы:
- 0°: Положительное направление оси x. В этой точке значение угла равно 0°.
- 90°: Положительное направление оси y. Значение угла равно 90°, когда луч пересекает положительное направление оси y.
- 180°: Отрицательное направление оси x. Угол равен 180°, когда луч пересекает отрицательное направление оси x.
- Между 0° и 90°: Углы между положительным направлением оси x и положительным направлением оси y.
- Между 90° и 180°: Углы между положительным направлением оси y и отрицательным направлением оси x.
Значение полярного угла от 0 до 180 градусов может быть использовано для определения положения точек в полярной системе координат, а также для описания направления и ориентации векторов и других физических величин.
Примеры использования полярного угла
1. Навигация
Полярные углы широко используются в навигации, особенно в морской и авиационной. Они позволяют определить направление и координаты объекта относительно определенной точки на плоскости. Например, при задании маршрута в авиации используются полярные углы для указания направления.
2. Фотография и видеозапись
Полярные углы могут использоваться в фотографии и видеозаписи для указания направления обзора камеры. Это особенно полезно при съемке панорамных фотографий или создании виртуальной реальности.
3. Радиосвязь
В радиосвязи полярные углы могут быть использованы для определения направления на источник сигнала. Это может быть полезно при поиске и ориентировании на радиостанцию или сигнал от другого устройства.
4. Физика и математика
Полярные углы широко применяются в физике и математике при решении задач, связанных с векторами, координатами и геометрией. Например, для описания движения тела в пространстве или определения координат точки на плоскости в полярной системе координат.
5. Радар и метеорология
В радарах полярные углы используются для определения направления объектов или целей. Также они применяются в метеорологии для описания формы и распределения облачности, так как позволяют задать направление и угол распространения облаков.
Полярные углы и теория вероятности
В теории вероятности полярные координаты и полярные углы широко применяются для описания вероятностных событий и распределений. Полярные углы играют важную роль при описании случайных величин, которые имеют угловую природу или зависят от углов.
Полярные углы обычно измеряются относительно оси, которая проходит через начало координат, и образуют полный оборот вокруг этой оси. Положительное направление обычно выбирается против часовой стрелки. Полярный угол может быть представлен в радианах или градусах.
Полярные углы могут использоваться для описания вероятностей в виде угловых распределений. Угловое распределение представляет собой вероятностное распределение случайной величины, измеряемой в полярных углах. Например, угловое распределение может быть использовано для моделирования направления ветра, направления движения частиц или ориентации объектов в пространстве.
Угловые распределения часто описываются с использованием функций плотности вероятности или кумулятивных функций распределения. Некоторые из наиболее известных угловых распределений включают равномерное распределение, нормальное распределение, косинусное распределение и фон-Нейманновское распределение.
| Распределение | Функция плотности вероятности | Функция распределения |
|---|---|---|
| Равномерное распределение |  |  |
| Нормальное распределение | 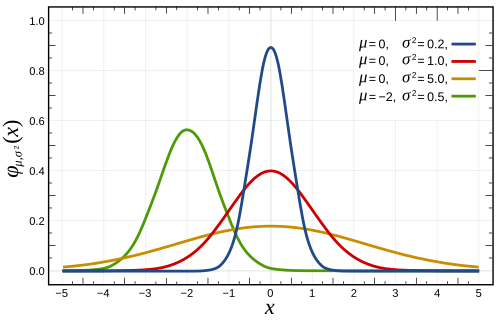 | 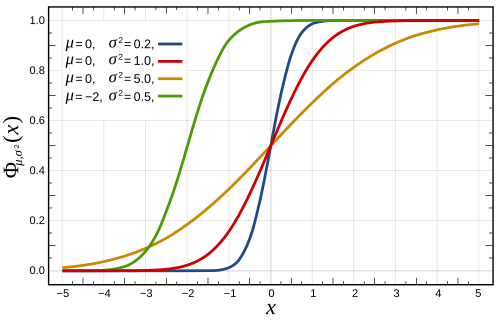 |
| Косинусное распределение |  |  |
| Фон-Нейманновское распределение |  |  |
Полярные углы и угловые распределения играют важную роль в различных областях, таких как статистика, машинное обучение, стохастическая геометрия и другие. Понимание основных свойств и применений полярных углов позволяет более точно моделировать и анализировать различные случайные процессы и явления.
Полярный угол в тригонометрии
Полярный угол – это специальный вид угла, который используется в полярной системе координат. В тригонометрии полярный угол представляет собой угол между положительным направлением оси абсцисс (положительным направлением оси X) и лучом, исходящим из начала координат в точку на плоскости.
Полярный угол измеряется в радианах или градусах и обычно обозначается греческой буквой φ (фи) или θ (тета). Особенность полярного угла заключается в том, что он имеет только одну меру от 0 до 360 градусов или от 0 до 2π радиан.
В тригонометрии полярный угол играет важную роль при описании и анализе положения точек на плоскости в полярной системе координат. Он позволяет определить радиус-вектор точки (расстояние от начала координат до точки) и направление вектора.
Основные свойства полярного угла в тригонометрии:
- Полярный угол может принимать значения от 0 до 360 градусов или от 0 до 2π радиан.
- Угол 0 градусов или 0 радиан соответствует направлению оси абсцисс.
- Угол 90 градусов или π/2 радиан соответствует направлению положительной оси ординат (ось Y).
- Угол 180 градусов или π радиан соответствует направлению отрицательной оси абсцисс.
- Угол 270 градусов или 3π/2 радиан соответствует направлению отрицательной оси ординат.
- Положительное изменение угла происходит против часовой стрелки, а отрицательное – по часовой стрелке.
Полярный угол – важный инструмент в тригонометрии, который позволяет удобно описывать и анализировать положение точек на плоскости в полярной системе координат. Знание свойств полярного угла поможет лучше разобраться в составляющих полярной системы координат и применить его при решении различных задач.
